The way that recsys is usually taught by starting from its taxonomy (collaborative filtering, content based, hybrid based) is confusing to me at first. In this post I am going to take another path to explain recsys by discussing the core components first and then draw the connection to the recsys taxonomy. Essentially, the majority of recsys objective is to map items and users on the same vector space through a learning objectives so that we can determine items to give to users for a recommendation or which items to show in a similar items page. My post is mostly based on this wonderful talk by James Kirk from Spotify so I highly recommend you to watch the video to gain further understanding.

Main components of a recommendation system:

Interactions Matrix
User and Item Features
User and Item Representation Function
Learning Objective
Prediction Function

Let’s go through it one by one!

Interaction Matrix

Interaction Matrix is the main components of a recsys, usually of \(M \times N\) size, where \(M\) is the number of users and \(N\) is the number of items. Note that user-item definition in a recsys is not restrictive to an actual user or item. The user is the receiving and acting entity on the recommendation, whereas the item is the passive entity that is being recommended to the user.

The matrix contains the interaction value between a user and an item. The interaction value can be:

positive (likes, 5-star review, purchases, views, etc) or negative (downvotes, 1-star review, skips, etc).
binary or continuous, depending on the data and the problem.
explicit or implicit. explicit interactions are usually an exact number given by the user (upvotes/downvotes, ratings, etd). implicit interactions are actions that are suggested but not stated clearly (views, clicks, counts, etc)

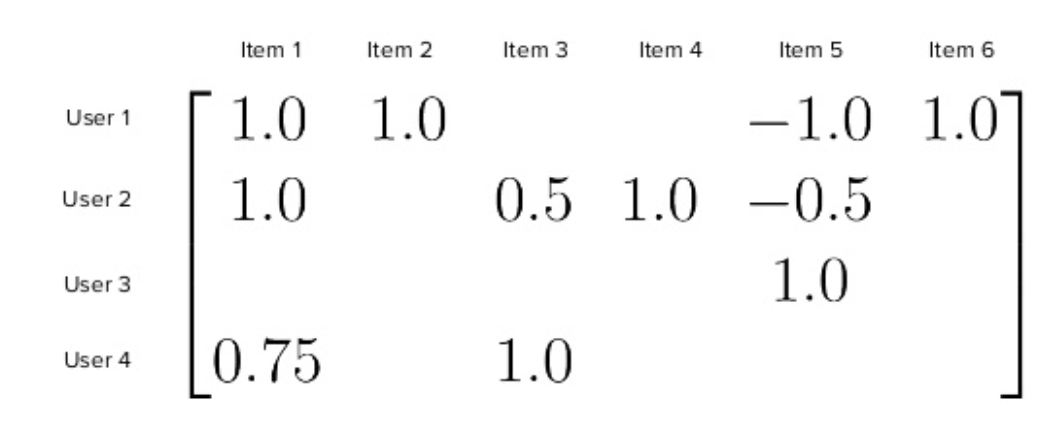
Source: James Kirk’s slides

Interaction value should reflect what is the intended effect that we want to happen in our recommender system. For example, if we want users to purchase more given our recommender system, then we want our interaction value to be related to purchase. If we want users to engage more in our platform, then our interaction value should be related to engagement.

We might also want to handle and preprocess our interaction matrix before using it. In some settings, users can give negative explicit interaction. Negative interactions can be a rich signals for the recsys to learn from but we need to be careful in handling them. Some loss functions such as learning-to-rank cannot accomodate negative signals. Interaction matrix is also usually sparse, so we need to handle missing value. In explicit interactions, we can’t just replace them with zeroes as it indicates that the user do not like the item. Hence we just go about modelling with sparse data. In implicit interactions, it is much safer to replace with zeroes as it indicates no action from the user (no views, no plays, etc). Missing values are usually what we want to predict with our recsys: giving item recommendation to a particular user that hasn’t been interacted by the user.

User/Item Features

There are two types of features in a recsys:

Indicator features: which represents user and item individually. The feature is unique to every user/item and encoded as one-hot vector. Since indicator is unique to every user/item, this feature does not scale to a lot of users. Indicator feature alone also cannot be used to solve cold-start problem (new users who does not have any interaction data).
Metadata features: any information that we know about user/item that can be incorporated to the recsys. Examples: age, gender, number of child, location, word embeddings, image representation, etc. In some cases, it might be beneficial to preprocess metadata features before using it in our recsys model. For example: converting any string/categorical metadata feature to a numerical type.

In a lot of libraries out there, if we do not specify any metadata features for item and user and use interaction matrix solely in our recsys, then by default only the indicator feature is used. The model is only going to learn representation that is unique for every user/item.

Source: James Kirk’s slides

Pure collaborative filtering is an approach where a recsys uses only indicator features.
Pure content-based filtering is an approach where a recsys uses only metadata features for the item and only indicator features for the user. Pure content-based does not share metadata features among users.
When both indicator and metadata features are used they’re known as a hybrid recsys.

User/Item Representation Function

In recsys we want to find a good representation for the user and item. A representation is typically a low-dimensional vector that encodes information regarding the user and item. Getting the representation involves transforming the user/item features via a representation function. Some examples of representation function:

Linear Kernels
Neural Networks (Fully Connected, Transformers, Word2vec, Autoencoder)
Passthrough (None)

Depending on the design, there are many ways to choose our representation function. Linear kernels are effective with both indicator and metadata features. Linear kernels are also a natural choice for matrix factorization problem. If we have an unstructured data, e.g., text/image that we want to utilize, we can use separate architecture like word2vec or autoencoder to get the text/image representation and then feed it into our recsys representation function. We can also use different representation function for different features, for example, linear kernels for indicator and metadata and passthrough for text/image (directly using representation output from the word2vec or autoencoder).

Prediction Function

A function that outputs the estimated items’ relevance to a particular user. This function converts user/item representation into a prediction. The prediction itself can vary depending on the design: it can be a score that tells us how relevant an item to a user but it can also be a relevance rank on several items for a particular user. Some examples of prediction function:

Dot product
Cosine similarity
Euclidian distance
Neural network

Learning Objective

This is essentially our loss function that let us uncover the best representation for the user/item. The learning objective converts both the user/item representation and prediction into a loss to learn the best parameter for the recsys model. Learning objective can have a huge impact on the output of the recommendation system. Changes in learning objective can dramatically affect how our recsys feel to the user. Examples of loss function characteristics:

Some loss functions learn to approximate the interaction value of a user-item and some loss functions learn to uprank positive interaction and downrank negative interactions for a particular user. The former predicts the interaction value and the latter predicts the ranking of items (learning-to-rank).
Some loss function accomodate negative interactions.
Some loss function are sensitive to interaction magnitude.
Some loss function only account for pairs with interactions (sparse), some loss can be made to compare every interaction pairs (dense), and some loss can learn by comparing pairs with interactions by sampling (sampled).

Due to these differences in nature, we must choose learning objective that best fit our goal. Some examples of loss function:

Root-mean-square error
KL Divergence
Alternating least square
Bayesian personalized ranking (learning-to-rank)
Weighted approximately ranked pairwise (learning-to-rank)

Combining it all together

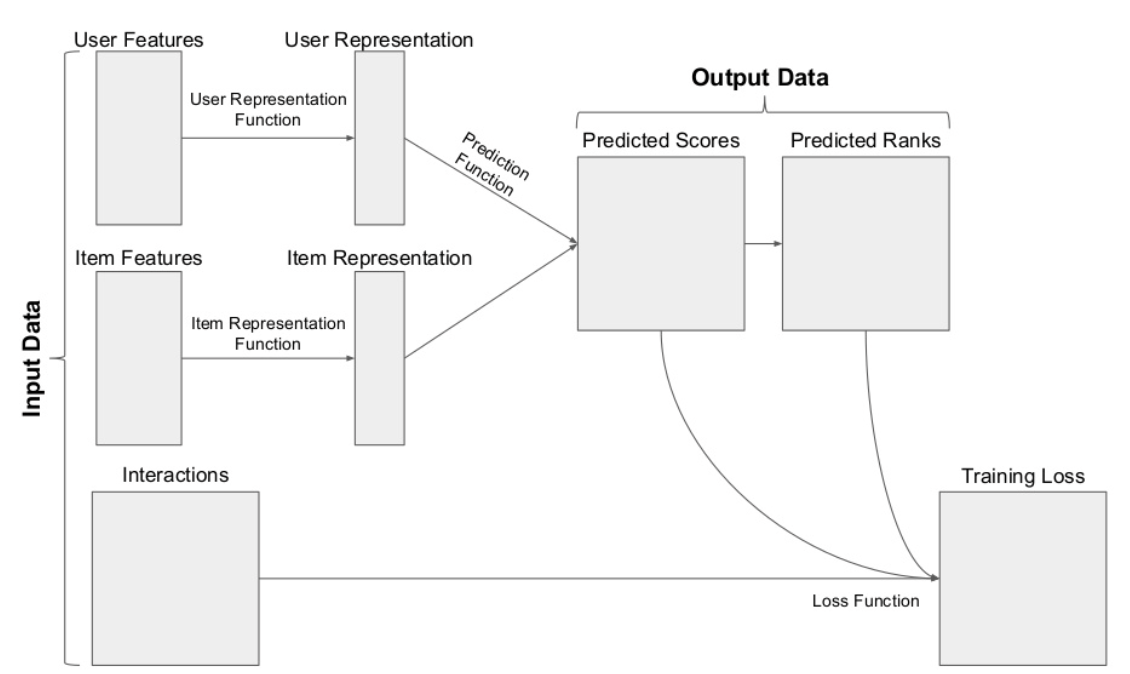
Common architecture of a recommender system. Source: James Kirk’s slides

There we have it: the architecture of recommender systems. Let’s try to design a recommender system based on some cases:

For you page. The example case is to recommend item on a homepage personalized for every user:

Interaction matrix: user-item (binary or continuous)
User features: indicator, metadata
Item features: indicator, metadata
User representation: linear
Item representation: linear
Learning objective: RMSE, binary cross entropy, WARP, BPE
Prediction function: dot product, cosine similarity

Similar items. The example case is to recommend item given another item:

Interaction matrix: item-item (binary or continuous)
User features: indicator, metadata
Item features: same as user features
User representation: linear
Item representation: linear
Learning objective: RMSE, binary cross entropy, WARP, BPE
Prediction function: dot product, cosine similarity

With this architecture, we can also incorporate more complex feature representation into the system. For example, if we want to utilize the social graph between user-user, then we can introduce graph neural network that takes an input of user graph (user features) and outputs the representation to be further processed (user representation).

For you page utilizing social graph structure:

Interaction matrix: user-item (binary or continuous)
User features: user-user graph
Item features: indicator, metadata, etc
User representation: graph neural network
Item representation: linear
Learning objective: custom RMSE
Prediction function: feed forward neural network

Simpler recsys such as user-based and item-based that does not require training also fits in this architecture. Let’s take a look:

User-based recsys:

Interaction matrix: user-item
User Features: Indicator but we use the row in the interaction matrix
Item Features: -
User representation: -
Item representation: -
Learning objective: -
Prediction function: dot product, cosine similarity. to predict the rating of an item \(y\) that user \(x\) hasn’t seen, we query top \(k\) users that are similar to user \(x\) (have rated item \(y\)) and calculate the weighted average of the ratings.

Item-based recsys:

Interaction matrix: user-item
User Features: -
Item Features: Indicator but we use the column in the interaction matrix
User representation: -
Item representation: -
Learning objective: -
Prediction function: dot product, cosine similarity. to predict the rating of an item \(y\) that user \(x\) hasn’t seen, we query top \(k\) users that are similar to item \(y\) (\(y\) has been rated by user \(x\)) and calculate the weighted average of the ratings.

Is there a recsys model that does not fit into this architecture?

Yes! In some cases we can use the interaction matrix to design the training data and not use it as our label. You can find some of the examples here where the author tries to create a pseudo-sentences of products to then be fed into a word2vec training. This setting does not use the interaction matrix as the label.

Thanks for reading! Contact me on twitter if you spot any mistake.